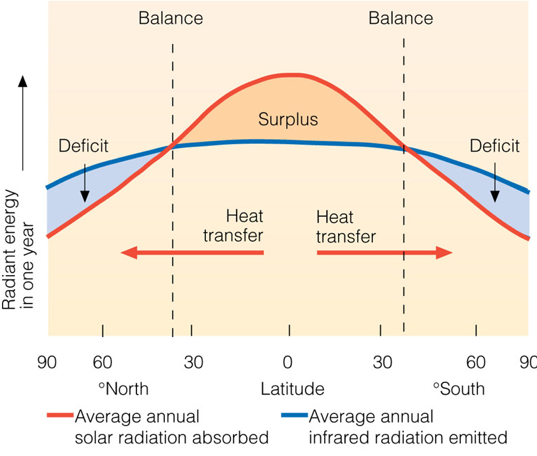
Earth's heat budget depends strongly on latitude. Part of this is Winds and ocean currents play a big role in redistributing heat.
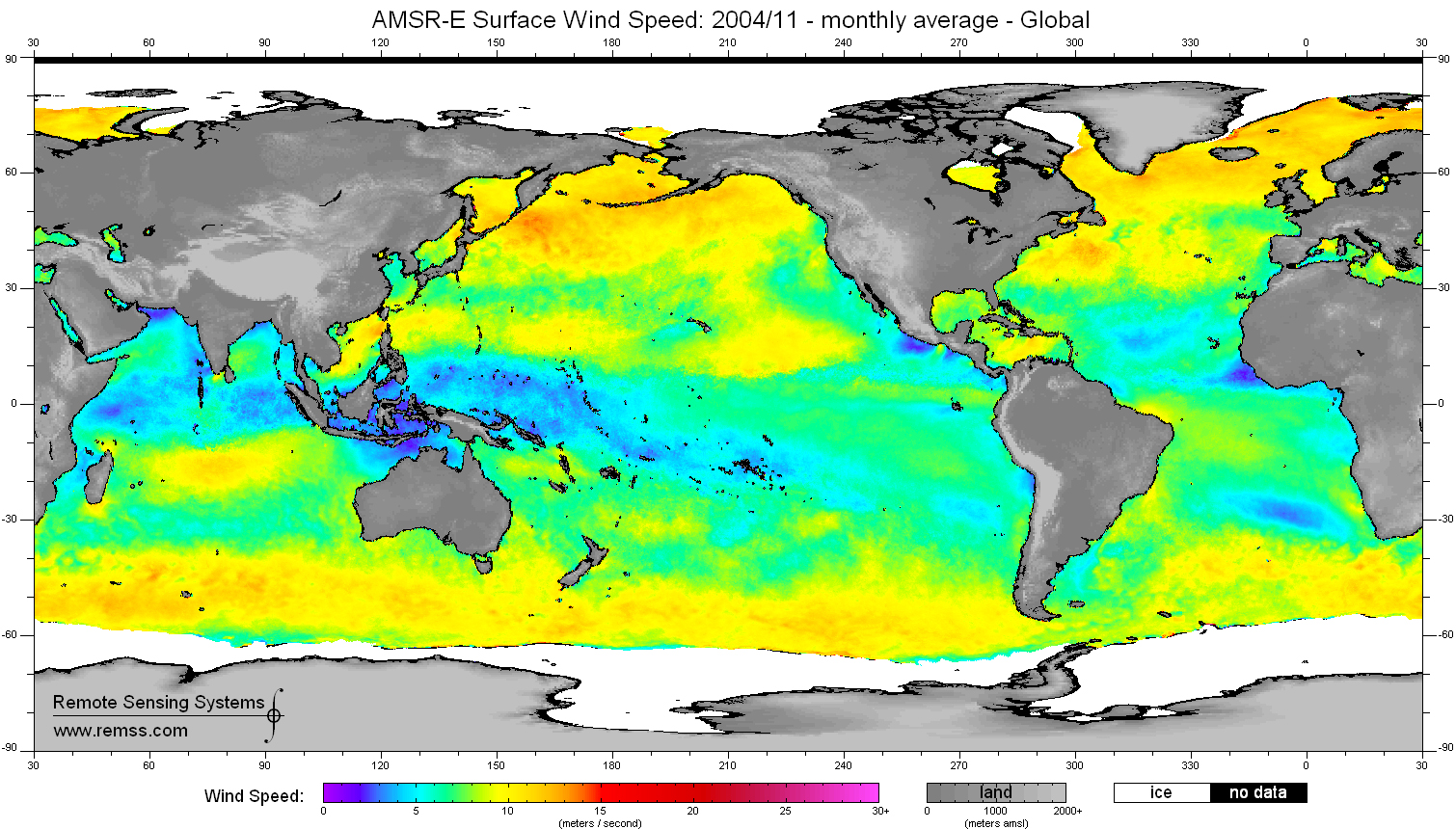
This figure shows sea surface wind speed, as derived from a NASA's satellite (Aqua) for the month of November 2004.

Earth's heat budget depends strongly on latitude. Winds and ocean currents play a big role in redistributing heat.
This figure shows sea surface wind speed, as derived from a NASA's satellite (Aqua) for the month of November 2004.
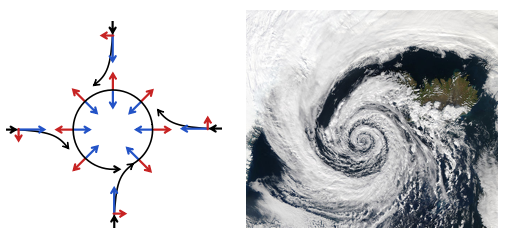
For large scale winds and ocean currents, the Coriolis effect is an important consideration because it changes the net direction of heat transport.
Coriolis Effect The Coriolis effect is due to an inertial force that is important in a rotating frame of reference. As you know from Newton's laws of motion, bodies in motion stay in motion unless acted upon by external forces. So, a wind blowing from north to south should go in a straight line, and in fact, it does. The problem is that this straight line does not look straight when referenced to a spinning Earth. There are many on-line resources for the Coriolis effect, so I won't try to duplicate visualizations here, but there are a few things to get straight before looking at a few of them.
1. The Coriolis force is given by the Coriolis acceleration times the mass of the object in motion. This is the familiar F = m a.
2. The Coriolis acceleration is proportional to the cross product between the (linear) velocity of the moving object and the angular velocity of the rotating frame of reference. On Earth, the angular velocity is given by 360 deg/24 Hr. or 2 π (radians) per 24 Hrs, which is equal to 1.454e-4 radians per sec. The formula is: ac = - 2ω x v
3. As you recall from plate tectonics and spherical trigonometry, the magnitude of a cross product like this can be obtained from the magnitude of each vector ( ω and v ) times the sin of the angle between them.
Thus, the magnitude of ac = ω v sinΔ where bold indicates magnitude and Δ is the solid angle between the vectors. For a three-dimensional body, this angle is a solid angle, and we can use the formulas developed from plate tectonics and spherical trigonometry to determine the solid angle. But fortunately, we don't need to use these, because the rotation axis corresponds to Earth's north pole, thus, we can just use the latitude.
If you want more background and examples, I can recommend the wikipedia page which is very well done.
I can also recommend: Coriolis explained
The left panel of the figure below is is an excellent summary of how the Coriolis effect (red arrows) combines with pressure driven wind (blue arrows) to produce the anticlockwise rotation (black arrows) around a low pressure system in the Northern Hemisphere What is the wind pattern, and sense of rotation, around a low pressure system in the Southern Hemisphere?
The right panel is a wonderful image of the wind pattern around a Low Pressure system over Iceland. Note the counterclockwise nature of the coiling pattern of the clouds. Does this look familiar from images that you've seen for hurricanes?
Read the link below.