LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Lesson 5 Overview

Introduction

In this lesson we will examine one of the most important methods in all of spatial analysis. Frequently data are only available at a sample of locations when the underlying phenomenon is, in fact, continuous and, at least in principle, measurable at all locations. The problem, then, is to develop reliable methods for 'filling in the blanks.' The most familiar examples of this problem are meterological, where weather station data are available, but we want to map the likely rainfall, snowfall, air temperature, and atmostpheric pressure conditions across the whole study region. Many other phenomena in physical geography are similar, such as soil pH values, concentrations of various pollutants, and so on.

The general name for any method designed to 'fill in the blanks' in this way is interpolation. It may be worth noting that the word has the same origins as extrapolation, where we use some observed data to extrapolate beyond known data. In interpolation, we extrapolate between measurements made at a sample of locations.

Learning Objectives

By the end of this lesson, you should be able to

1. explain the concept of a spatial average and describe different ways of deciding on inclusion in a spatial average
2. describe how spatial averages are refined by inverse distance weighting methods
3. explain why the above interpolation methods are somewhat arbitrary and must be treated with caution
4. show how regression can be developed on spatial co-ordinates to produce the geographical technique known as trend surface analysis
5. explain how a variogram cloud plot is constructed and, informally show how it sheds light on spatial dependence in a dataset
6. outline how a model for the semi-variogram is used in kriging and list variations on the approach
7. make a rational choice when interpolating field data between inverse distance weighting, trend surface analysis, and geostatistical interpolation by kriging
8. explain the conceptual difference between interpolation and density estimation

Reading Assignment

The reading this week is again quite detailed and demanding, and again, I would recommend starting early. You need to read the following:

• Section 8.3, "Spatial Interpolation," pages 220-234
• Chapter 9, "Knowing the Unknowable: The Statistics of Fields" (more advanced methods of interpolation, in particular trend surface analysis and kriging), pages 246-83
• Section 2.4, "Preview: The Variogram Cloud and the Semivariogram," pages 45-49

It is OK if you're reading of Chapter 9 is a little less thorough than for other parts of this course, as the primary aim here is that you develop a knowledge of the methods covered in that chapter at an overview level, rather than at the level of all the grisly mathematical detail.

After you've completed the reading, or at the very least skimmed the material, get back online and supplement your reading from the commentary material, then test your knowledge with the self-test quizzes.

Lesson 5 Deliverables

This lesson is one week in length. The following items must be completed by the end of the week. See the Calendar tab, above, for the specific date.

1. Complete the two self-test quizzes satisfactorily (you have an unlimited number of attempts and must score 90% or more).
2. Complete Project 5, which involves working with interpolation methods in a GIS setting. (The materials for Project 5 can be found under the Lessons tab, in the Lesson 5 folder.)
3. Continue the Quarter-long Project by providing commentary on two of your colleagues' project proposals as described in the Week 5 directions. (This link opens in a new window. The materials for the Quarter-long Project can be also be found under the Lessons tab.)

Questions?

If you have any questions now or at any point during this lesson, please feel free to post them to the Lesson 5 thread on the Lesson Content Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the Communicate tab, above, and then scrolling down to the Discussion Forums section.)

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Commentary - Chapter 8, Section 8.3, "Spatial Interpolation"

The Basic Concept

A key idea in statistics is estimation. A better word for it (but don't tell any statisticians I said this...) might be guesstimation, and a basic premise of much estimation theory is that the best guess for the value of an unknown case, based on available data about similar cases is the mean value of the measurement for those similar cases.

This is not a completely asbtract idea: in fact, it is an idea we apply regularly in everyday life.

I'm reminded of Christmas time, when quite a few packages might be arriving at the house. When I take a box from the mail carrier, I am prepared for the weight of the package based on the size of the box. If the package is much heavier than is typical for a box of that size, I am surprised, and have to adjust my stance to cope with the weight. If the package is a lot lighter than I expected then I am in danger of throwing it across the room! More often than not, my best guess based on the dimensions of the package works out to be a pretty good guess.

So, the mean value is often a good estimate or 'predictor' of an unknown quantity.

Introducing Space

However, in spatial analysis, we ususally hope to do better than that, because of a couple of things:

1. Near things tend to be more alike than distant things (this is spatial autocorrelation at work), and
2. We have information on the spatial location of our observations.

Combining these two observations is the basis for all the interpolation methods described in section 8.3. Instead of using simple means as our predictor for the value of some phenomenon at an unsampled location, we use a variety of locally determined spatial means, as outlined in the text.

In fact, not all of the methods described are used all that often. By far the most commonly used in contemporary GIS is an inverse-distance weighted spatial mean (pages 223-32).

Limitations

It is important to understand that all of the methods described in section 8.3 share one fundamental limitation, mentioned on page 229, but not emphasized. This is that they cannot predict a value beyond the range of the sample data. This means that the most extreme values in any map produced from sample data, will be values already in the sample data, and not values at unmeasured locations. It is easy to see this by looking at the example below, which has been calculate using a simple average of the nearest 5 observations to interpolate values.

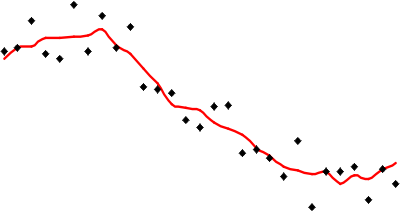
Red line is the interpolated value (i.e., vertical position) based on a simple average of the nearest 5 sample values.

It is apparent that the red line representing the interpolated values is less extreme than any of the sample values represented by the point symbols. This is a strong assumption made by simple interpolation methods that kriging attempts to address (see later in this lesson).

Distinction Between Interpolation and Kernel Density Estimation

Pay close attention to the box on page 234 ("Interpolation and Density Estimation"). It is easy to get interpolation and density estimation confused, and in some cases the mathematics used is very similar, adding to the confusion. The important distinction is the intention behind employing each method.

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Commentary - Chapter 9, Section 9.2, "Review of Regression"

Regression is the basis of another method of spatial interpolation— trend surface analysis—so before looking at that, we will review regression. The discussion of regression in section 9.2 may be a little technical for some tastes. If you can handle it, so much the better—I find this visual treatment of regression very helpful in understanding how regression works.

On the other hand, if you are wondering, "What the heck's regression?," here is the two minute summary—which is more than adequate for present purposes.

Simple linear regression is a method that models the variation in a dependent variable (y) by estimating a best-fit linear equation in an independent variable (x). The idea is that we have two sets of measurements on some collection of entities. Say, for example, we have data on the mean body and brain weights for a variety of animals. We would expect that heavier animals will have heavier brains, and this is confirmed by a scatter plot:

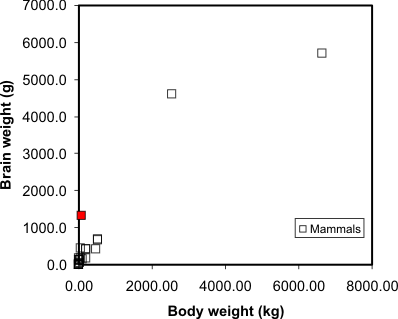
Scatter plot of animal brain weights relative to their body weight. Humans are the red square (which is reassuring). Source: P. J. Rousseeuw and A. M. Leroy (1987) Robust Regression and Outlier Detection. Wiley, p. 57.

A regression model makes this visual relationship more precise, by expressing it mathematically, and allows us to estimate the brain weight of animals not included in the sample data set. Visually, the regression equation is a trendline in the data (in fact, in many spreadsheet programs, you can determine the regression equation by adding a trendline to an X-Y plot, as I have done here):

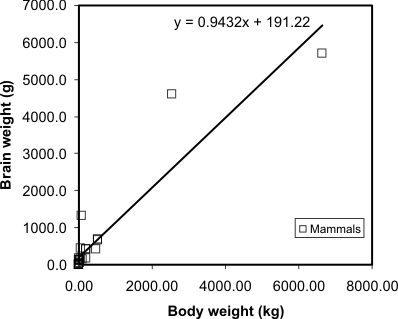
Regression line and equation added to the mammal brain weight data. Source: P. J. Rousseeuw and A. M. Leroy (1987) Robust Regression and Outlier Detection. Wiley, p. 57.

... and that's all there is to it! It is occasionally useful to know more of the underlying mathematics of regression, but the important thing is to appreciate that it allows the trend in a data set to be described by a simple equation.

A postscript...

Completely irrelevant, but it is sort of fun: the same dataset (below) contains similar data for three species of dinosaurs, and is quite revealing:

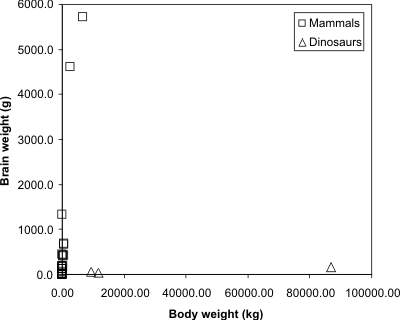
The same dataset, but with three dinosaurs included. Source: P. J. Rousseeuw and A. M. Leroy (1987) Robust Regression and Outlier Detection. Wiley, p. 57.

It is apparent that for all their enormous size, some dinosaurs at least had quite tiny brains (comparable to those of present day kangaroos or sheep, which are far from the smartest of animals).

But I digress...

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Commentary - Chapter 9, Section 9.3, "Regression on Spatial Coordinates: Trend Surface Analysis"

With even a basic appreciation of regression, the idea behind trend surface analysis is very clear. Treat the observations (temperature, height, rainfall, population density, whatever they might be) as the dependent variable, in a regression model that uses spatial coordinates as its independent variables.

This is a little more complex than simple regression, but only just. Instead of finding an equation

            z = b₀ + b₁ x,

where z are the observations of the dependent variable, and x is the independent variable, we find an equation

            z = b₀ + b₁ x + b₂y,

where z is the observational data, and x and y are the geographic coordinates of locations where the observations are made. This equation defines a plane, as shown in figure 9.4 (page 257).

In fact, trend surface analysis finds the underlying first order trend in a spatial dataset (hence the name).

As an example of the method, the image below shows the settlement dates for a number of towns in Pennsylvania as vertical lines such that longer lines represent later settlement. The general trend of early settlement in the southeast of the state around Philadelphia to later settlement heading north and westwards is evident.

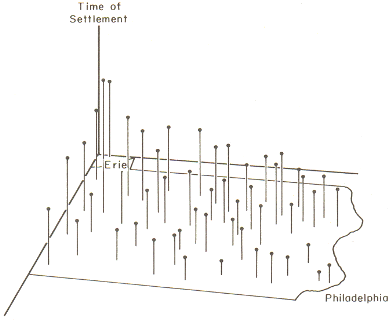
Settlement times of Pennsylvania towns shown as vertical lines. Source: Abler, Ronald F., John S. Adams, and Peter Gould. Spatial Organization the Geographer's View of the World. Englewood Cliffs, NJ: Prentice-Hall, 1971, page 135.

In this case, latitude and longitude are the x and y variables, and time of settlement is the z variable.

When trend surface analysis is conducted on this dataset, we obtain an upward sloping mean time of settlement surface that clearly reflects the evident trend, and we can draw isolines (contour lines) of settlement date:

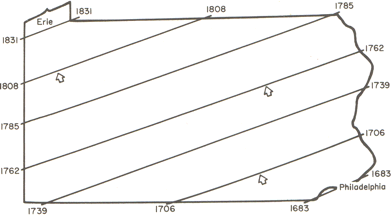
Isolines for the time of settlement trend surface. Source: Abler, Ronald F., John S. Adams, and Peter Gould. Spatial Organization the Geographer's View of the World. Englewood Cliffs, NJ: Prentice-Hall, 1971, page 136.

While this confirms the evident trend in the data, it is also useful to look at departures from the trend surface, which, in regression analysis are termed residuals or errors.

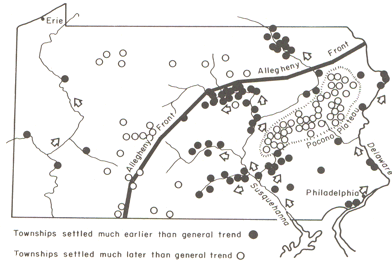
In this view, black filled settlements were settled well before the general trend, and open circles indicate settlements formed later than the general trend. Source: Abler, Ronald F., John S. Adams, and Peter Gould. Spatial Organization the Geographer's View of the World. Englewood Cliffs, NJ: Prentice-Hall, 1971, page 136.

The role of the physical geography of the state is evident in the pattern of early and late settlement, where most of the early settlement dates are along the Susqehanna River valley, and many of the late settlements are beyond the ridge line of the Allegheny Front.

This is a relatively unusual application of trend surface analysis. It is much more commonly used as a step in universal kriging, when it is used to remove the first-order trend from data, so that the kriging procedure can be used to model the second-order spatial structure of the data.

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Commentary - Chapter 2, Section 2.4, "Preview: The Variogram Cloud and the Semivariogram"

[Note that the jump here to Section 2.4 is intentional!]

We have seen how simple interpolation methods use locational information in a dataset to improve estimated values at unmeasured locations. We have also seen how a more 'statistical' approach can be used to reveal first order trends in spatial data. The former approaches makes some very simple assumptions about the ' first law of geography' in order to improve estimation. The latter approach uses only observed patterns in the data to derive spatial patterns. The last approach to spatial interpolation that we consider combines both methods by using the data to develop a mathematical model for the spatial relationships in the data, and then uses this model to determine the appropriate weights for spatially weighted sums.

The mathematical model for the spatial relationships in a dataset is the semivariogram. The sequence of steps outlined in section 2.4 (pages 45-9) and then extended in section 9.4 (pages 266-74) describes how a semivariogram function may be fitted to a set of spatial data.

It is not important in this course to understand the mathematics involved here in great detail. It is more important to understand the aim, which is to obtain a concise mathematical description of some of the spatial properties of the observed data, which may be used to improve estimates of values at unmeasured locations.

You can get a better feel for how the variogram cloud and the semivariogram work by experimenting with the Geostatistical Analyst extension in ArcGIS, which you will do in this week's project.

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Commentary - Chapter 9, Section 9.4, "Statistical Approach to Interpolation: Kriging"

The Semivariogram, pages 266-74

This long and complex section builds on section 2.4 by first giving a more complete account of the semivariogram. Particularly noteworthy are:

• Figure 9.7 (page 270) repays careful study. It shows how the semivariogram summarizes three aspects of the spatial structure of the data:
  1. The local variability in observations, in a sense, the uncertainty of measurements, regardless of spatial aspects is represented by the nugget value;
  2. The characteristic spatial scale of the data is represented by the range. At distances greater than the range observations are of little use in estimating an unknown value;
  3. The underlying variance in the data is represented by the sill value.
• The 'cautionary tale' (pages 273-4) is also important, and shows what happens if there is a strong first order trend to a dataset. The semivariogram shows this by not 'leveling off' to a sill value. Because of the trend, the further apart are any two observations, the more different they will be. We cope with this by modeling the trend using trend surface analysis, subtracting the trend from the base data to get residuals, and then fitting a semivariogram to the residuals.

Kriging, pages 274-81

If you have a strong background in mathematics you may relish the discussion of kriging, otherwise you will most likely be thinking, "Huh?!" If that's the case, don't panic! It is possible to carry out kriging without fully understanding the mathematical details, as we will see in this week's project. If you are likely to use kriging a lot in your work, I would recommend finding out more from one of the references in the text (Isaaks and Srivastava's book is particularly good, and amazingly readable given the complexities involved).

LESSON 5: INTERPOLATION - FROM SIMPLE TO ADVANCED

Final Activities for Lesson 5

Now that you've completed the readings and self-test quizzes for this lesson, it is time to apply what you've learned!

The following links will open in a new browser window.

1. Complete Project 5, which involves working with interpolation methods in a GIS setting. (When you are done reviewing this Web page, click on the "Next" link, above, to begin Project 5. The materials for Project 5 can also be found under the Lessons tab, in the Lesson 5 folder.)
2. Continue the Quarter-long Project by providing commentary on two of your colleagues' project proposals as described in the Week 5 directions. (This link opens in a new window. The materials for the Quarter-long Project can be also be found under the Lessons tab.)

PROJECT 5: INTERPOLATION METHODS

Overview

Background

This week and next we'll work on data from Central Pennsylvania, where Penn State's University Park campus is located. This week we'll be working with elevation data showing the complex topography of the region. Next week, we'll see how this ancient topography affects the contemporary problem of determining the best location for a new high school.

Introduction

The aim of this week's project is to give you some practical experience with interpolation methods, so that you can develop a feel for the characteristics of the surfaces produced by different methods.

To enhance the educational value of this project, we will be working in a rather unrealistic way, because you will know at all times the correct interpolated surface, namely the elevation values for part of central Pennsylvania (the part that is home to Penn State, as it happens). This means that it is possible to compare the interpolated surfaces you create with the 'right' answer, and to start to understand how some methods produce more useful results than others. In real-world applications, you don't have the luxury of knowing the 'right answer' in this way, but it is a useful way of getting to know the properties of different interpolation methods.

In particular, we will be looking at how the ability to incorporate information about the spatial structure of a set of control points into kriging, using the semivariogram, can significantly improve the accuracy of the estimates produced by interpolation.

To further enhance your learning experience, this week I would particularly encourage you to contribute to the project Discussion Forum. There are a lot of options in the settings you can use for any given interpolation method, and there is much to be learned from asking others what they have been doing, suggesting options for others to try, and generally exchanging ideas about what's going on. I will contribute to the discussion when it seems appropriate. Remember that a component of the grade for this course is based on participation, so if you've been quiet so far, this is an invitation to speak up!

Project Resources

The data files you need for Project 5 are available here in a zip archive file. If you have any difficulty downloading this file, please contact me.

• project5materials.zip

That file is 3.3 Mb and will take approximately 8 minutes to download over a 56 Kbps modem. Once you have downloaded the file, double-click on the project5materials.zip file to launch WinZip, PKZip, 7-Zip, or another file compression utility. Follow your software's prompts to decompress the file. Unzipping this archive you should get an ArcMap project file (centreCounty.mxd), a geodatabase file (centralPA.mdb) and a folder containing topographic data layers (topo). Open the ArcMap file to find layers as follows:

• pacounties - the counties of Pennsylvania
• centreCounty - Centre County Pennslyvania, home to Penn State
• pa_topo - a DEM at 500 meter resolution showing elevations across Pennsylvania
• majorRoads - major routes in Centre County
• localRoads - local roads, which allow you to see the major settlements in Centre County, particularly State College in the south, and Bellefonte, the county seat, in the center of the county
• allSpotHeights - this is a point layer of all the spot heights derived from the statewide DEM

Summary of Project 5 Deliverables

For Project 5, the items you are required to submit are as follows:

• What accounts for this unusual 'spiky' distribution? How do you think the data for this DEM were derived? Post suggestions to the Project 5 Open Thread on the project Discussion Forum and I'll let you know when someone has figured it out.
• Make an interpolated map using the inverse distance weighted method. Insert this map into your write-up, along with your commentary on the advantages and disadvantages of this method, and a discussion of why you chose the settings that you did.
• Make a layer showing the error at each location in the interpolated map. You may present this as a contour map over the actual or interpolated data if you prefer. Insert this map into your write-up, along with your commentary describing the spatial patterns of error in this case.
• Make two maps using simple kriging, one with an isotropic semivariogram, the other with an anisotropic semivariogram. Insert these into your write-up, along with your commentary on what you learned from this process. How does an anisotropic semivariogram improve your results?

\\

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Project 5 thread on the Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the In Touch tab, above, and then scrolling down to the Discussion Forums section.)

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Something Odd About DEMs That Is Worth Noting...

Before we get started, an aside.

Take a look at the histogram below:

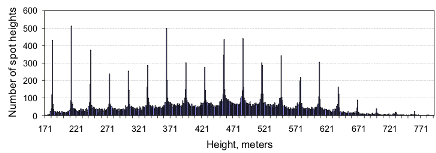
Histogram of the spot heights in the allSpotHeights data set

This shows the numbers of spot heights with each of the various possible heights in the data range (from 171 to 792 meters in this case).

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Making A Random Spot Height Dataset

In this case, we have a 500 meter resolution DEM, so that interpolation would not normally be necessary, assuming that this was adequate for our purposes. In this section, I will explain how to create a random set of spot heights derived from the DEM, so that we can work with those spot heights to evaluate how well different interpolation methods reconstruct the original data. Note that there is an alternative approach using the Data Management - Create Random Points and the Spatial Analyst - Extraction - Extract By Points tools in the Arc Toolbox. If you have the appropriate licences (Arc/INFO, then you can experiment with using these instead to generate around 600 spot heights, as described below).

Follow the steps below, using the centralPA.mxd file:

1. Right-click on the allSpotHeights layer and select the Open Attribute Table... option from the pop-up menu. The layer's attribute table will open.
2. Right-click on the heading of the column labeled Selector, and select the Calculate Values... option.
   
   

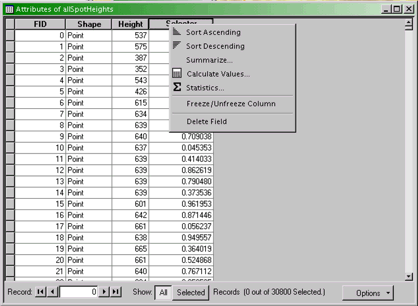
   The attribute table for the allSpotHeights layer.

3. Ignore the message about doing calculations outside an edit session and continue to the Field Calculator dialog. Enter a calculation so the Selector variable is calculated from the expression rnd(), as shown below.
   

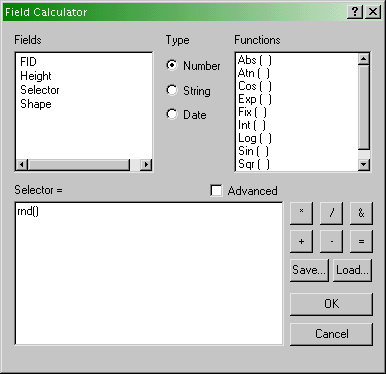
   Field Calculator dialog showing the calculation required in this case (see text).

4. Click OK. The Selector values in the attribute table for allSpotHeights will change.
5. Now, perform a selection operation on the allSpotHeights layer, using Select by Attribute... with Selector > 0.98 . This will select around 600 spot heights at random from the full data set. You should export these to make a new shape file, which you use in the remainder of this project to perform interpolation.
   
   A typical random selection of spot heights is shown below.

   

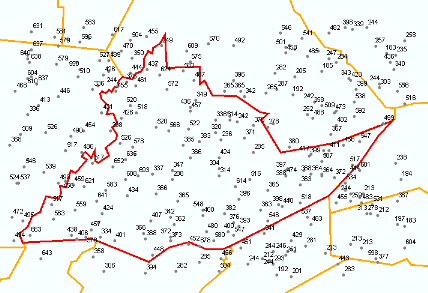
   A random set of spot heights for use in subsequent parts of this project

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Inverse Distance Weighted Interpolation (1)

Preliminaries

Before doing any interpolation, it is important to ensure that the Spatial Analyst extension is enabled in ArcMap and that you have sensible settings for the ArcMap Spatial Analyst.

To enable the Spatial Analyst:

1. Select the menu item Tools - Extensions... and enable the Spatial Analyst.
2. Right-click on the toolbar and enable the Spatial Analyst toolbar.

To setup the Spatial Analyst options:

1. Select the Spatial Analyst - Options... menu item.
2. In the General tab, set an appropriate temporary Working directory, choose the allSpotHeights layer for the Analysis mask, and choose to save the analysis results in the same coordinate system as the data frame (the second option).
3. In the Extent tab, set the analysis extent to Same as Layer "allSpotHeights".
4. In the Cell Size tab set the Cell size to 500.

Performing inverse distance weighted interpolation

1. Once the Spatial Analyst is set up correctly, it is a simple matter to perform inverse distance weighted interpolation. Select the Spatial Analyst - Interpolate to Raster - Inverse Distance Weighted... menu option. The dialog below will appear.

   

   Specify the inverse distance weighted interpolation parameters here

2. Here you specify various options as discussed in the text:
   • Input points specifies the layer containing the control points.
   • Z value field specifies which attribute of the control points you are interpolating.
   • Power is the inverse power for the interpolation. 1 is a simple inverse (1 / d), 2 is an inverse square (1 / d ²). You can set a value close to 0 (but not 0) if you want to see what simple spatial averaging looks like (as discussed on pages 225-7 of the text).
   • Search radius type specifies either Variable radius defined by the number of points or Fixed radius defined by a maximum distance.
   • Search radius settings. Here you defined Number of points and Maximum distance as required by the Search radius type you are using..
   • Output cell size. This setting should be defined in the Spatial Analyst - Options as 500 (see above).
   • Output raster. To begin with, it's worth requesting a <Temporary> output until you get a feel for how things work. Once you are more comfortable with it, you can specify a file name for permanent storage of the output as raster dataset.
3. Experiment with these settings until you have a map you are happy with.

Make an interpolated map using the inverse distance weighted method. Insert the map into your write-up, along with your commentary on the advantages and disadvantages of this method and a discussion of why you chose the settings that you did.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Inverse Distance Weighted Interpolation (2)

Creating a map of interpolation errors

The Spatial Analyst doesn't create a map of errors by default (why?) but in this case, we have the correct data, so it is instructive to compile an error map to see where your interpolation output fits well and where it doesn't.

1. Use the Spatial Analyst - Raster Calculator... menu option to bring up the Raster Calculator dialog:

   

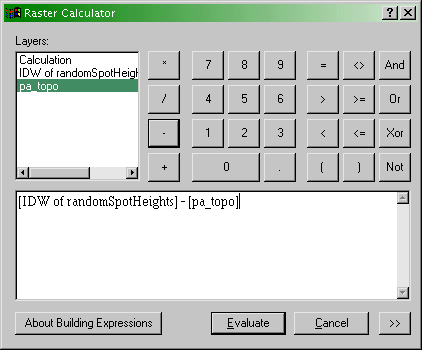
   The Spatial Analyst Raster Calculator dialog. Here you can define operations on raster map layers such as calculating the error in your interpolation output (see text).

2. The error at each location in your interpolated map is ( interpolated elevation - actual elevation). It is a simple matter to enter this equation in the expression editor section of the dialog, as shown. When you click Evaluate, you will get a new raster layer showing the errors, both positive and negative, in your interpolation output.
3. Using the Spatial Analyst - Surface Analysis - Contour... tool, you can draw error contours and examine how these relate to both your interpolated and actual elevation maps. Where are the errors largest? What are the errors at or near control points in the random spot heights layer? What feature of these data does inverse distance weighted interpolation not capture well?

Make a layer showing the error at each location in the interpolated map. You may present this as a contour map over the actual or interpolated data if you prefer. Insert the map into your write-up, along with your commentary describing the spatial patterns of error in this case.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Kriging Using The Geostatistical Analyst

Preliminaries

Before you can use the Geostatistical Analyst, you have to enable it. Use the Tools - Extensions... menu and right-click on the toolbar to ensure that the Geostatistical Analyst is available.

'Simple' kriging

We use the Geostatistical Wizard to run kriging analyses. Access the wizard from the Geostatistical Analyst - Geostatistical Wizard... menu item. The wizard consists of a series of screens, which are explained below.

1. The Geostatistical Wizard: Choose Input Data and Method dialog

   

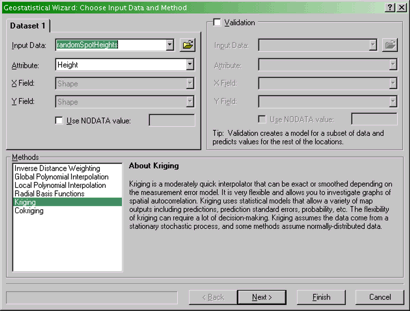
   The first screen of the Geostatistical Wizard. Specify the data set and method to use here.

   
   Here you specify the Input Data (your random spot heights layer) and Attribute (Height) that you are interpolating. You also specify the Method to use. Select Kriging from the list, and then click Next >.
2. The Geostatistical Wizard Step 1 of 4 - Geostatistical Method Selection dialog

   

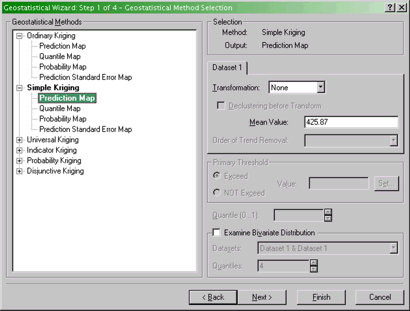
   Specifying the exact method of kriging.

   
   In this dialog you select from a number of different kriging methods and the type of output you are interested in. Select a Simple Kriging Prediction Map. Click Next >.
3. The Geostatistical Wizard Step 2 of 4 - Semivariogram / Covariance Modeling dialog

   

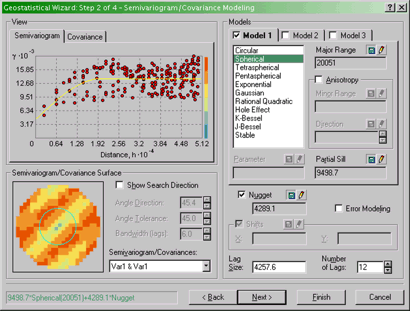
   Specifying the semivariogram model to work with in kriging.

   
   Here you should select the Semivariogram tab, and you can select a function to fit from the long list available to the right of the graphical display. You can experiment with these, although I would recommend sticking with one of the first five or six, since the later ones are slow to calculate...and it's debatable how much of a difference it makes!
   
   There is also an option here to specify assuming Anisotropy in constructing the semivariogram (you may want to refer back to the readings in the text on this!). This will be important later, when it comes to the deliverables for this part of the project.
   
   When you are finished experimenting, click on Next >.
4. The Geostatistical Wizard Step 3 of 4 - Searching Neighborhood dialog

   

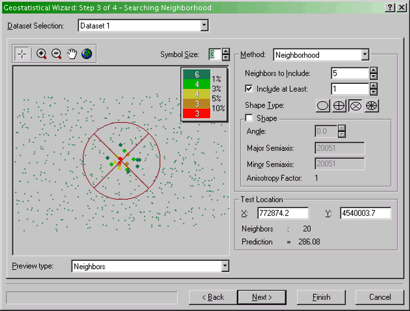
   Specifying properties of the search neighborhood for kriging.

   
   Here you can get previews of what the interpolated surface will look like given the currently selected parameters. Switch between a view showing the neighbors included in each local estimate and a preview of the interpolated surface by selecting Neighbors or Surface from the Preview type drop-down list.
   
   Also specify how many neighbors to include using the Method: Neighborhood options. You can specify how many Neighbors to Include in the local estimates and also how they are distribute around the location to be estimated using the Shape Type options. The button applies a simple limit on the number of neighbors in all directions. The various 'pie slice' buttons, , define several regions around the location which are each required to contain the required number of neighboring control points as specified by the Neighbors to Include option. You can get a feel for how these controls affect the calculation using the Neighbors preview.
   
   After this stage, click Finish. (We won't be going into the other step in the Wizard, although you can try it, if you like!) The Geostatistical Analyst makes a new layer and adds it to the map. You will find it helpful in comparing this layer to the 'correct' result (i.e., the pa_topo layer) to right-click on it and adjust its Symbology so that only contours are displayed.

Things to do...

The above steps have walked you through the rather involved process of creating an interpolated map by kriging. What you should do now is simply specified, but may take a while experimenting with various settings.

Make two maps using simple kriging, one with an isotropic semivariogram, the other with an anisotropic semivariogram. Insert these into your write-up, along with your commentary on what you learned from this process. How (if at all) does an anisotropic semivariogram improve your results?

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 5: INTERPOLATION METHODS

Checklist of Project 5 Deliverables

Here is a summary of the deliverables for Project 5, to be posted as a PDF (preferably) or MS Word document. Once posted, please provide a link to the document in the discussion forum "Posted project links" thread for this week. Note that if you don't have access to any webspace for posting, that you can simply attach the document to your post to the discussion forum. Make sure you have completed each item!

1. What accounts for this unusual 'spiky' distribution? How do you think the data for this DEM were derived? Post suggestions to the Project 5 Open Thread on the project Discussion Forum and I'll let you know when someone has figured it out.
2. Make an interpolated map using the inverse distance weighted method. Insert this map into your write-up, along with your commentary on the advantages and disadvantages of this method, and a discussion of why you chose the settings that you did.
3. Make a layer showing the error at each location in the interpolated map. You may present this as a contour map over the actual or interpolated data if you prefer. Insert this map into your write-up, along with your commentary describing the spatial patterns of error in this case.
4. Make two maps using simple kriging, one with an isotropic semivariogram, the other with an anisotropic semivariogram. Insert these into your write-up, along with your commentary on what you learned from this process. How does an anisotropic semivariogram improve your results?

That's it for Project 5!

End of Project 5 - Remember, if you have any questions, post them to the appropriate Discussion Forum.

QUARTER-LONG PROJECT

Week 5: Finishing the Peer Review Process

Last week you were assigned two other students' project proposals to review. This week you should be finishing up your reviews, which are due by the end of the week. Timely submission of your reviews is worth 4 of the 30 total points available for the quarter-long project.

Refer back to the Week 4 directions if you need a reminder of the kinds of comments you should provide in your reviews.

Use Post your comments on each assigned project proposal to the 'Project Initial Proposal discussion board' as responses to the messages announcing your assigned projects. Your peer reviews are due by the end of this week (midnight end of the day, Tuesday).

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Quarter-long Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the In Touch tab, above, and then scrolling down to the Discussion Forums section.)

That's it for the quarter-long project this week!