LESSON 6: SURFACE ANALYSIS

Lesson 6 Overview

Introduction

Once you have field data, whether as a result of interpolation, or based on more complete original data, perhaps from aerial surveys or remote-sensed imagery, you will likely want to analyze it in a variety of ways. In this lesson, we look at the fundamentals of such analysis and in the project explore the application of such methods to field data.

Learning Objectives

By the end of this lesson, you should be able to

1. describe data models for field data: regular grid, triangulated irregular network, closed form mathematical function, control points; and discuss how the choice of model may affect subsequent analysis
2. explain the map algebra concept and describe focal operations, local operations and between-map operations
3. understand the idea of slope and aspect as a vector field
4. explain how slope or gradient can be determined from a grid of height values
5. describe how surface aspect may be derived from a grid of height values
6. re-express these operations as local operations in map algebra
7. describe how map algebra operations can be combined to develop complex functionality

Reading Assignment

You need to read the following selections from the textbook:

• Section 8.2, "Modeling and storing field data," pages 213-20
• Section 8.4, "Derived measures on surfaces," pages 234-42

The course text does not cover all the material we need, so there is some information in the commentaries for this lesson that is not covered at all in the textbook reading assignments. In particular, read carefully the online information for this lesson on "Map Algebra" and "Vector Fields."

After you've completed the reading, get back online and supplement your reading from the commentary material, then test your knowledge with the self-test quiz.

Lesson 6 Deliverables

This lesson is one week in length. The following items must be completed by the end of the week. See the Calendar tab, above, for the specific date.

1. Complete the self-test quiz satisfactorily (you have an unlimited number of attempts and must score 90% or more).
2. Complete Project 6, where you will apply surface analysis methods, including more complex map algebra operations, to the problem of choosing a suitable location for a new high school. (The materials for Project 6 can be found under the Lessons tab, in the Lesson 6 folder.)
3. Continue the Quarter-long Project revising your proposal in light of comments received, and submitting it. See the Week 6 directions for details. (This link opens in a new window.)

Questions?

If you have any questions now or at any point during this lesson, please feel free to post them to the Lesson 6 thread of the Lesson Content Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the Communicate tab, above, and then scrolling down to the Discussion Forums section.)

LESSON 6: SURFACE ANALYSIS

Commentary - Chapter 8, Section 8.2, "Modeling and Storing Field Data"

Continuous phenomena and field data

It is always important in the context of geospatial data to distinguish between the phenomenon itself and its representation in data. This is especially so with data that represent phenomena theoretically measurable at all locations but in practice only measured at sample locations. The phenomenon (say atmospheric pressure) could, in principle, be measured at every location on Earth, but in practice it cannot be. Instead, we work with a set of measurements at control points and interpolate these to generate a field that approximates the continuous phenomenon. How the control points and any subsequent interpolation results are stored can have important effects on subsequent analysis steps.

On pages 214-20 a variety of methods for storing field data are discussed, and some of their advantages and disadvantages considered. The schemes you are most likely to encounter in practice are point sampling schemes of one kind or another, particularly grid-based samples. Grid-based sampling schemes are particularly useful as the basis for surface analysis operations, because the equally-spaced measurements simplify many mathematical operations. Further, since any other surface data can be readily converted to this format by interpolation, in the remainder of this lesson we assume that field data are available as a grid.

However, it is important to bear in mind that grids of field values often did not start out that way, but were produced by interpolation from a much sparser set of control points. As a consequence of this, you should check any associated metadata before assuming the accuracy of data values in a grid.

LESSON 6: SURFACE ANALYSIS

Commentary - Map Algebra

"Map Algebra" is material not covered in the course text.

Map algebra is a framework for thinking about analytical operations applied to field data. It is most readily understood in the case of field data that are stored as a grid of values, but is in principle applicable to any type of field data.

The map algebra framework was devised by Dana Tomlin and is presented in his 1990 book Geographical Information Systems and Cartographic Modeling (Prentice Hall: Englewood Cliffs NJ), which you should consult for a more detailed treatment than is given here. Another good reference on map algebra (and much else besides) is GIS Modeling in Raster (Wiley: New York, 2001) by Michael DeMers.

Many GISs (including ESRI ArcGIS) support map algebra. In ArcMap, the tool most closely related to map algebra is called the 'map calculator'.

Basic concepts

The fundamental concepts in map algebra are exactly as in mathematical algebra, that is

• Values are the 'things' on which the algebra operates. Input data and output data (results) are presented as grids of values. Note, that as has already been discussed, values can be categorical ( nominal or ordinal) or numerical.
• Operators may be applied to values to transform them, or between two or more values to produce a new value. In mathematical algebra the minus sign '' is an operator that negates a single value when placed in front of it, as in 5. The plus sign '+' is also an operator, signifying the addition operation, which, when applied between two values, produces a new value: 1 + 2 = 3
• Functions are more complex, but still well defined operations, that produce a new value from a set of input values. The input set may be a single value, as in log₁₀({100}) = 2, or a set of values, as in average({1, 2, 3, 4}) = 2.5.

Now consider two small grids of values:

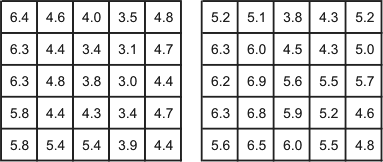
Two small grids of values representing typical data fields

If we want to apply an operation or function to these values, how should we proceed? It is apparent that we have a number of options, and map algebra clearly defines these as described in the following sections. Note that we refer to these grids as [left_grid] and [right_grid] when necessary in the discussion.

Local operations and functions

A local operation or function in map algebra is simply applied to each individual cell value in isolation. For example, the local negation operation signified by the minus sign '' and applied to the left hand grid above grid results in the following output grid, [left_grid]:

Result of the local negation operation applied to [left_grid] from the previous figure

Applying a local operation between two grids involves applying the operation to values in corresponding positions in each grid, and recording the result in the corresponding position in the output grid. For example the result of the + operation applied between the two grids above is, [left_grid] + [right_grid]:

Result of the local addition operation applied between [left_grid] and [right_grid]

Another example is a local maximum operation between two (or more) grids, which assigns to each output location the maximum of the values at the corresponding location in the input grids. The result of local_max( [left_grid] , [right_grid] ) applied to the two example grids above is:

Result of the local_max operation applied to [left_grid] and [right_grid]

Focal operations and functions

We can also apply an operator, or, more often, a function, focally to a grid. This means that the value at each location in the output grid is arrived at by combining values focused at the corresponding location in the input grid or grids. A simple example is focal_max which would assign to each output location the maximum of the values in the that location and its immediate neighbors in the input grid. The result of applying a focal maximum function to left_grid is:

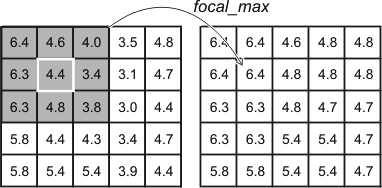
Result of the focal_max( [left_grid] ) function. The result at each location in the output grid is determined from the set of values at that location and neighboring locations in the input grid, as shown by the shading.

Many functions can be applied focally in this way, such as maximum, minimum, mean (or average), median, standard deviation, and so on. In addition to the function itself, the output grid will depend on how the focal neighborhood is defined in a particular case. In the above example, the focal neighborhood is the grid cell itself and the eight immediate neighbors. Some alternative neighborhood definitions are shown below:

Some alternative definitions of the focal neighborhood relative to the central cell of this small grid.

A different choice of focal neighborhood will alter the output grid that results when a focal function is applied. Notice that there is no requirement that the neighborhood be symmetrical about the focal grid cell, as shown in the last example. A non-symmetrical neighborhood like this might have application in understanding how air pollution spreads given a prevailing wind direction.

Zonal operations and functions

Zonal operations and functions are an extension of the focal concept. Rather than define operations with respect to each grid cell, a set of map zones are defined (for example, counties) and operations or functions are applied with respect to these zones. You have already seen an example of a zonal function in practice in the Texas redistricting project in lesson 1, where estimated numbers of voters for each party were summed for Congressional Districts.

Global operations and functions

Finally, some operations and functions are global, meaning that the values at each grid cell in an output grid may potentially depend on the values at all grid cell locations in the input grid(s). An operation that finds the cost (in time or money) of the shortest path from a specified location (say a school) to every other location may have to take into account values at all locations in a grid to find the correct answer (travel cost might be based on the land cover type and its slope).

LESSON 6: SURFACE ANALYSIS

Commentary - Vector Fields

"Vector Fields" is covered in the text, but in a number of different places.

So far in this course, we have only considered attribute data types that are single-valued whether that value is categorical or numerical. In spatial analysis, we frequently encounter attributes that are not conveniently represented in this way. In particular, we may need to use vectors to represent some types of data.

A vector is a quantity that has both value (or magnitude) and direction. The most obvious vector in real life application is wind, which has a speed (its magnitude or strength), and direction. Without wind direction information, wind speed information is not very useful in many applications. For example, an aircraft navigator needs to know both wind speed and direction to accurately plot a course, and to estimate arrival times, or fuel requirements.

As mentioned in the text (pages 236-7), the most fundamental vector field is the gradient field associated with any scalar (i.e., simple numerical) field. This often has practical applications. For example, the gradient field of atmospheric pressure is important in meteorology in determining the path of storm systems and wind directions.

LESSON 6: SURFACE ANALYSIS

Commentary - Chapter 8, Section 8.4, "Derived Measures on Surfaces"

The measures discussed in this section are just a small sample of the types of surface analysis measure that can be devised. In this commentary, we focus on how these can be expressed as map algebra operations.

Relative relief

Relative relief, from the definition on page 235 in the text, is readily expressed as a map algebra function:

rel_relief = focal_max( [elevation] )  focal_min( [elevation] )

where the focal region is defined accordingly.

Surface gradient and aspect

Surface gradient is more complex, requiring a number of steps. First, two focal functions to calculate the slope in two orthogonal directions must be defined. These will be similar functions, but must have specially defined focal areas that pick out the immediately adjacent grid cells on either side of the focal cell in each of the two cardinal directions.

If these slopes are called ew-gradient (for east-west) and ns-gradient (for north-south), then the overall gradient is given by

gradient = square-root( ( arctan( ew-gradient ) )² + ( arctan( ns-gradient ) )² )

and the overall aspect is given by

aspect = arctan( ( ew-gradient ) / ( ns-gradient ) )

These examples should give you a feel for the flexibility of the map algebra framework. In this week's project you will have an opportunity to explore map algebra more thoroughly in a more practical setting.

LESSON 6: SURFACE ANALYSIS

Final Activities for Lesson 6

Now that you've completed the readings and the self-test quiz for this lesson, it is time to apply what you've learned!

The following links will open in a new browser window.

1. Complete Project 6, where you will apply surface analysis methods, including more complex map algebra operations, to the problem of choosing a suitable location for a new high school. (When you are done reviewing this Web page, click on the "Next" link, above, to begin Project 6. The materials for Project 6 can also be found under the Lessons tab, in the Lesson 6 folder.)
2. Continue the Quarter-long Project revising your proposal in light of comments received, and submitting it. See the Week 6 directions for details. (This link opens in a new window - the materials for the Quarter-long Project can be also be found under the Lessons tab.)

PROJECT 6: RASTER MAP ANALYSIS

Overview

Background

Now let's continue our work on data from Central Pennsylvania, where Penn State's University Park campus is located. This week we'll see how this ancient topography affects the contemporary problem of determining potential locations for a new high school.

Introduction

The Centre region of Pennsylvania is the fastest growing region in the state, largely as a result of the presence of Penn State in the largest town of State College. Growth is putting pressure on many of the region's resources, and some thought is currently being given to the provision of high schools in the region. In this project we will use raster analysis based on road transport in the region to determine potential sites for a new school. This will demonstrate how complex analysis tasks can be performed by combining results from a series of relatively simple analysis steps.

Project Resources

The data files you need for Project 6 are available here in a zip archive file. If you have any difficulty downloading this file, please contact me.

• project6materials.zip

That file is 1.65 Mb and will take approximately 4 minutes to download over a 56 Kbps modem. Once you have downloaded the file, double-click on the project6materials.zip file to launch WinZip, PKZip, 7-Zip, or another file compression utility. Follow your software's prompts to decompress the file. Unzipping this archive you should get an ArcMap project file (centreSchools.mxd ), a geodatabase file (centreSchools.mdb) and a folder containing topographic data layers (topo). Open the ArcMap file to find layers as follows:

Layers in the ArcMap file (centreSchools.mxd) are as follows:

• highSchools - four high schools in Centre County, Pennsylvania
• centreCountySchoolDistricts - the corresponding school districts
• majorRoads - major roads in the region
• localRoads - minor roads in the region
• centreCountyCivilDivisions - showing townships and boroughs in the county
• representativePopInSchoolDistricts - a point layer derived from census block group centroids with attributes for total population and children aged between 5 and 17
• centreBGdemographics - more complete demographic data from the 2000 census associated with polygons representing the block groups for which the data were collected
• centretopo100 - the topography of the county at 100 meter resolution.

Summary of Project 6 Deliverables

For Project 6, the items you are required to have in your write-up are:

• Describe in your write-up how the distance analysis operation works, including commentary on how you would combine multiple distance analyses results (one for each high school) to produce an allocation analysis output and the differences in the straight line distance allocation and the actual allocation of places to school districts in the present example.
• Describe in your write-up how you created the roads raster.
• Perform the cost weighted distance analysis for high schools using the roads raster layer. Examine the resulting allocation layer. How does it differ from the straight-line distance allocation result? Do the roads account for all the inconsistencies between the straight line distance allocation and the actual school districts? Answer these questions in your write-up.
• Estimate the number of the school age children in the four school districts, and also in the road travel cost weighted distance allocation zones associated with each school, and put these estimates in your write-up. Also describe how you arrived at your estimates.
• Insert into your write-up a map and other details of your proposals for a new high school and associated district, including arguments for and against, possible problems with your analysis, maps, and explanations of any analysis carried out.

 

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Project 6 thread on the Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the Communicate tab, above, and then scrolling down to the Discussion Forums section.)

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

Allocation Based on Straight Line Distance

As in last week's project, you should ensure that the Spatial Analyst - Options... are set appropriately before doing any analysis. In particular use the centreCountyCivilDivisions layer as an Analysis mask and for the Extent. Also set the Temporary working directory to something sensible and choose to save the analysis results in the same coordinate system as the data frame (the second option).

The first analysis we will do uses a built-in function of the Spatial Analyst to allocate each part of the map to the closest one of a set of points. This is the raster equivalent of proximity polygons.

1. Select the Spatial Analyst - Distance... - Straight Line Distance... menu option.

   

   The Straight Line dialog with parameters set to generate an allocation of areas to high schools.

   Running straight line distance analysis will produce two layers, a distance layer, and an allocation layer. The distance layer will look something like this:

   

   Results of the straight line distance analysis for high schools

   While the allocation layer should look like this:

   

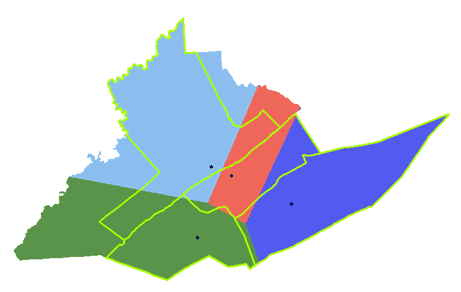
   Results of the straight line distance allocation

2. You can further analyze these layers. For example, it may be easier to read the distance analysis if you create contour lines. The results of the allocation analysis can be converted to vector polygons, which may make subsequent analysis operations easier to perform.

Describe of how the distance analysis operation works in your Project 6 write-up. In your description, comment on how you would combine multiple distance analyses results (one for each high school) to produce an allocation analysis output. Finally, comment on the differences in the straight line distance allocation and the actual allocation of places to school districts. (You will need to look at the roads, topography, and minor civil divisions to make sense of this.)

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

Distance Analysis Over Roads (1)

Clearly roads are a major factor in the difference between straight line distance allocation of school districts, and actual school districts. In this part of the project you will create a raster layer representing the roads of Centre County to use in a second roads-based distance analysis.

Creating a roads raster layer using map algebra operations

1. Using the Spatial Analyst - Convert - Features to Raster... tool make raster layers from the majorRoads and localRoads layers.
2. Use the Spatial Analyst - Reclassify... and Spatial Analyst - Raster Calculator... tools, to manipulate and combine these layers into a single roads layer where major road cells have value 1, minor road cells have value 2, and off-road cells have some high value (say 100).

   This is a multistep operation—you will have to create intermediate Calculation layers and combine those in various ways to arrive at something like this:.

   

   Part of a roads raster layer. Red cells have value 1, orange cells have value 2, and clear (that is, background color) cells have value 100.

Describe how you created the roads raster in your Project 6 write-up.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

Distance Analysis Over Roads (2)

Using the roads raster layer for distance analysis

Distance analysis using a roads raster layer is straightforward. The values in the layer are regarded as 'weights' indicating how much more expensive it is to traverse that cell than if the cell were unweighted. Thus, with the roads layer just created, traveling on major roads incurs no penalty, travelling on local roads is twice as expensive (takes twice as long), and traveling off-road is very slow indeed (100 times slower). These are not accurately determined weights, but serve to demonstrate the potential of these methods.

1. Select the Spatial Analyst - Distance... - Cost weighted... option to bring up the Cost Weighted dialog:

   

   The dialog used to specify parameters for distance analysis to high schools over the road network

2. Now, you should repeat the previous distance analysis, but weighted by the roads raster layer you created. Also, request an Allocation output from the analysis. (If you are interested in later experimenting with the Distance.. Shortest path... tool you should also request a Direction output, but this is not required for the project.)

Perform the cost weighted distance analysis for high schools using the roads raster layer. Examine the resulting allocation layer. How does it differ from the straight-line distance allocation result? Do the roads account for all the inconsistencies between the straight line distance allocation and the actual school districts? Respond to these questions in your Project 6 write-up.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

Allocation Based on Road Distances

Estimating school age population in each school district

1. Using the Spatial Analyst - Zonal Statistics tool you can estimate the number of age 5 to 17 children in each school district:

   

   Specify here the dataset containing the zones for which you want to compile summary statistics for a raster dataset.

2. To prepare for this you will need to create a raster layer representing the school age population for the region. There are a number of options available, starting with either the representativePopInSchoolDistricts point data, or the centreBGdemographics polygon layer. Whatever way you do it, use the AGE_5_17 variable as an approximation for the count of school age children.

Estimate the number of the school age children in the four school districts, and also in the road travel cost weighted distance allocation zones associated with each school, in your Project 6 write-up. Include a description of how you arrived at your estimates.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

And so... where to put a new school, and what should be its district?!

The headline above summarizes the last part of the project. Based on the analyses already carried out, and any other analyses required to support your answer, locate a new high school in Centre County!

As a minimum you should use the ArcMap editing tools to add a school to the highSchools layer and create a map of the new school, and what the new school's associated district would be. You should insert this map together with a description of how you arrived at it into your Project 6 write-up. Note that school districts are always made up of a contiguous collection of townships and/or boroughs, and that the centreCountyCivilDivisions layer shows these.

Insert into your Project 6 write-up a map and other details of your proposals for a new high school and associated district, including arguments for and against, possible problems with your analysis, maps, and explanations of any analysis carried out.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 6: RASTER MAP ANALYSIS

Checklist of Project 6 Deliverables

Here is a summary of the deliverables for Project 6, to be posted as a PDF (preferably) or MS Word document. Once posted, please provide a link to the document in the discussion forum "Posted project links" thread for this week. Note that if you don't have access to any webspace for posting, that you can simply attach the document to your post to the discussion forum. Make sure you have completed each item!

1. Describe how the distance analysis operation works, including commentary on how you would combine multiple distance analyses results (one for each high school) to produce an allocation analysis output and the differences in the straight line distance allocation and the actual allocation of places to school districts in the present example.
2. Describe how you created the roads raster.
3. Perform the cost weighted distance analysis for high schools using the roads raster layer. Examine the resulting allocation layer. How does it differ from the straight-line distance allocation result? Do the roads account for all the inconsistencies between the straight line distance allocation and the actual school districts? Respond to these questions in your write-up.
4. Estimate the number of the school age children in the four school districts, and also in the road travel cost weighted distance allocation zones associated with each school. Also desribe how you arrived at your estimates.
5. Insert into your write-up a map and other details of your proposals for a new high school and associated district, including arguments for and against, possible problems with your analysis, maps, and explanations of any analysis carried out.

That's it for Project 6!

End of Project 6 - Remember, if you have any questions, post them to the appropriate Discussion Forum.

QUARTER-LONG PROJECT

Week 6: Revising Your Project Proposal

Based on the comments you received from other students and from me, revise your original project proposal and submit a final version this week. Timely submission of your revised project is worth up to 6 of the 30 total points available for the quarter-long project. Note that you may lose points if your proposal suggests that you haven't been developing your thinking about your project.

In your revised proposal you should try to respond to as many of the comments made by your reviewers as possible. However, it is OK to stick to your guns! You don't have to adjust every aspect of the proposal to accommodate reveiwer concerns, but you should consider every point seriously, not just ignore them.

Your final proposal should be between 600 and 800 words in length and should include the same items as before:

• Topic and scope
• Aims
• Data
• Data sources
• Intended analysis and outputs -- This is a little different from before. It should list some specific outputs (ideally several specific items) that can be used to judge how well you have done in attaining your stated aims. Note that failing to produce one of the stated outputs will not result in an automatic loss of points, but you will be expected to comment on why you were unable to achieve everything you set out to do (even if that means simply admitting that some other aspect took longer than anticipated, so you didn't get to it).

Post your revised (final) project proposal to your web site, as part of the "Quarter-long Project" section of your site. Use the course email system to notify the instructor that you have done this including a URL.

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Quarter-long Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the In Touch tab, above, and then scrolling down to the Discussion Forums section.)

That's it for the quarter-long project this week!