LESSON 8: SPATIAL AUTOCORRELATION

Lesson 8 Overview

Introduction

The most basic observation to be made about spatial data is that it typically exhibits spatial structure. In statistical terms, this translates to the observation that spatial data are not random. Knowing something about a phenomenon at some location A, often tells us a great deal about the same phenomenon at a location not far away from A. Another way of putting this is that spatial data sets are correlated with themselves over distance.

When two variables x and y are correlated, then given the value of x for a particular case, I can make a good estimate of the likely value of y for that case. Similarly, given information about the value of some attribute measured at spatial location A, then I can often make a reasonable estimate of the value of the same attribute at a nearby location to A. This is due to spatial autocorrelation (spatial self-correlation).

Much of the material we have studied so far in this course makes use of spatial autocorrelation in data, whether it is assumed or measured. Perhaps the best example is interpolation (see Lesson 5) where we use information only from nearby control points to inform our calculation of an estimated value at a location where no observation has been recorded. We do this because we expect nearby data to be more relevant than distant data. In kriging, this is taken one step further when one method of measuring spatial autocorrelation--the semivariogram--is used to improve further the estimates produced by an interpolation method.

In this week's lesson we look in a more general way at the various approaches that spatial analysts and geographers have developed for measuring spatial autocorrelation.

Learning Objectives

By the end of this lesson, you should be able to

1. define autocorrelation with reference to Tobler's 'first law' of geography and distinguish between first and second order effects in a spatial distribution
2. differentiate between isotropic and anisotropic spatial distributions
3. justify, compute and test the significance of the joins count statistic for a pattern of area objects
4. compute Moran's I and Geary's c for a pattern of attribute data measured on interval or ratio scales
5. explain the importance of spatial weights matrices to the development of autocorrelation measures and variations of the approach, particularly lagged autocorrelation
6. explain how autocorrelation measures can be generalized to compute and map Local Indices of Spatial Association (LISA)
7. describe how Monte Carlo methods may be used to determine significance for LISA

Reading Assignment

The reading this week is all in Chapter 7. You need to read the following selections from the textbook:

• Section 7.4, "Spatial Autocorrelation: Introducing the Joins Count Approach," pages 180-92
• Section 7.5, "Fully Worked Example: The 2000 US Presidential Election," pages 192-6
• Section 7.6, "Other Measures of Spatial Autocorrelation," pages 196-203
• Section 7.7, "Local Indicators of Spatial Association," pages 203-5

After you've completed the reading, get back online and supplement your reading from the commentary material, then test your knowledge with the self-test quizz.

Lesson 8 Deliverables

This lesson is one week in length. The following items must be completed by the end of the week. See the Calendar tab, above, for the specific date.

1. Complete the self-test quiz satisfactorily (you have an unlimited number of attempts and must score 90% or more).
2. Complete Project 8. This week's project explores ethnic residential segregation in Auckland, New Zealand using spatial autocorellation measures provided by the GeoDa tool. (The materials for Project 8 can be found under the Lessons tab, in the Lesson 8 folder.)
3. Continue the Quarter-long Project by posting evidence of your progress this week. See the Week 8 directions for details. (This link opens in a new window.)

Questions?

If you have any questions now or at any point during this lesson, please feel free to post them to the Lesson 8 thread on the Lesson Content Discussion Forum.(That Discussion Forum can be accessed at any time by clicking on the Communicate tab, above, and then scrolling down to the Discussion Forums section.)

LESSON 8: SPATIAL AUTOCORRELATION

Commentary - Chapter 7, Section 7.4, "Spatial Autocorrelation: Introducing the Joins Count Approach"

In this section the simplest method of measuring autocorrelation is described: the joins count statistic. In practice, joins counting is not used much, but understanding the basis for this approach will enable you to understand the similar ideas underlying other methods.

A good place to start is actually halfway through the text; look at figure 7.5 on page 187. This is probably the most readily understood description of the meaning of positive, negative, and no autocorrelation. In a positively autocorrelated map, like cases are grouped together, so that, on average, map units are of the same type as their neighbors. In a negatively autocorrelated map, map units of different types are mixed among one another, the most extreme case being the checkerboard illustrated in figure 7.5 part (c). In this case, knowing what type one map unit is tells us immediately that any of its neighbors is of the opposite type. Students often have difficulty understanding that an uncorrelated map is simply a random one, not a negatively correlated one.

Just to emphasize the point, patterns that are not as clear cut as those in figure 7.5 can be positively autocorrelated because each square tends to have similar neighbors, even if the overall arrangement is 'random'.

A more realistic example of positive autocorrelation: units are likely to be the same as their neighbors, but the overall pattern is a randomly shaped configuration.

Similarly, negative autocorrelation is a tendency for map units to differ from their neighbors. It does not occur only in a perfect checkerboard:

A negatively autocorrelated map. Parts of this map are 'checkerboard-like' but some parts are not.

Finally, an uncorrelated, or random map, is simply that: random. Both cases below are random maps. Altough each has regions which we might designate as positively (or negatively) autocorrelated, there is no overall tendency for like or unlike cells to be neighbors.

Two random patterns. The one on the left tends toward positive autocorrelation, while the one on the right tends to negative autocorrelation. Both were generated completely at random.

It is exactly this 'fuzziness' in the nature of autocorrelation that calls for precisely defined ways of measuring the phenomenon.

Runs in Serial Data or One-Dimensional Autocorrelation

Before we go on to two-dimensional (i.e., spatial) data it is conceptually easier to develop a method for assessing autocorrelation in serial data. A series of coin flips or draws from a deck of cards is the example used in the text. More 'real world' examples might be records of whether or not the maximum temperature one day was higher than that the day before. A similar idea would be whether a market index was up or down each day (or week or month). A less serious, but just as familiar, example is the case of sports teams in a 'streak' of success (or failure). In the United States the most familar example is 'streaky' shooting from the free throw line in basketball. Using the runs count statistic, it is possible to test whether or not there are statistical grounds for considering any of these examples of streaks as unusual or not.

The runs count idea is very simple. Each unbroken sequence of a particular outcome is considered as a 'run' of that outcome. This reduces a sequence such as

HHTTTHTHHTTHTHHHH

to

HH ₁ TTT ₂ H ₃ T ₄ HH ₅ TT ₆ H ₇ T ₈ HHHH ₉

where the subscripts count the runs of ( underlined) like outcomes. In this case, there are nine runs. As explained on pages 183-6 this result can be assessed statistically to determine if it is unusual relative to what we would expect from a random sequence of outcomes.

In this case, using equation (7.22) on page 185, we can say that we would expect 8 runs with a standard deviation of 2. This allows us to say that the observed number of runs, at 9, is really not very unusual, since it has an associated z score of (9 - 8) / 2 = 0.5, which is well within the bounds of what we would expect to see by chance variation. It's worth noting that this is the case even though there is one run of three tails, and one of four heads in this sequence (which some people might find surprising).

The trickiest concept here is the distinction between non-free and free sampling. As noted in the text, in geographic examples we are usually dealing with a situation where it would be unreasonable to assume an analogy to flipping a coin when examining the state of a set of geographic units. Rather, it is more correct to consider them analogous to drawing from a deck of cards with known numbers of units of each type.

Extending Runs Counting to Two Dimensions: The Joins Count

Of course, we aren't really interested in flipping coins or drawing cards from a deck, but rather in developing a way of measuring how strongly a map is patterned. As discussed in the text, a close cousin of the runs count idea applied to map patterns is joins counting. Instead of counting the number of sequences of like cases, we count the different types of neighboring pairs of interest. In a two-type situation (blacks and whites) there are three types of neighboring pairs or joins: black-black, white-white, and black-white (in either order).

In a positively autocorrelated case, where like is near like, there will be large numbers of black-black and white-white joins and relatively few black-white joins. In a negatively autocorrelated case, with different type map units frequently neighbors, black-white joins will predominate.

Whether any particular map pattern is unusual with respect to the expected numbers of joins of the different types can thus be reduced to a statistical calculation, where we first count the joins of various types, then calculate the expected numbers of joins of each type, then convert the observed numbers to z scores so that we can assess how unusual they are and whether they are high or low.

The hardest thing here is to get to grips with the k and m factors that are used in the various complex equations on pages 188-90. k is straightforward, being simply the total number of joins on the map. m is less obvious. Its calculation is shown as an equation (7.26). For each map unit, we count its neighbors and multiply this number by the same number minus one. We then sum all these results up and multiply by one-half to arrive at the value for m used in calculation of the standard deviations in equation (7.25).

All should become clear in the worked example in the following section.

LESSON 8: SPATIAL AUTOCORRELATION

Commentary - Chapter 7, Section 7.5, "Fully Worked Example: The 2000 U.S. Presidential Election"

The central aspect of the calculation is shown in figure 7.7 on page 194. This adjacency matrix (remember back in Lesson 1?) records for each state which states are its neighbors. From this matrix the k and m parameters can be calculated. Since k is simply the total number of joins in the map, it is given by the total number of '1's in the matrix divided by two (since each join appears twice in the matrix). Calculation of m is done by totaling the number of '1's in each row of the matrix (e.g. for Tennessee, in row 24, there are 8) multiplying by one less than this number (in this case 8 × 7 = 56), then summing all these products for all rows in the matrix and dividing by two. The result is 440. You can see that these calculations are much better handled by a computer than by an error-prone human being.

Once k and m have been determined, the next step is to calculate expected numbers of joins of each type based on some probability model for the occurrence of states of each type. The simplest approach is to use a free-sampling model (perhaps not the best method, certainly the easiest). Using the noted numbers of votes for each candidate we arrive at the stated expected joins counts of each type recorded equation (7.35) on page 195.

These are substantially different from the observed joins counts stated in equation (7.36) on page 195.

There are many more BB joins, somewhat fewer WW joins, and many fewer BW joins than expected.

All of these results are consistent with positive autocorrelation in the map, since more BB joins (a like with like neighboring pair) and fewer BW joins (a like with unlike neighboring pair) both support the idea that similar outcomes are likely in neighboring map units.

This basic observation is confirmed statistically when we convert the observed joins counts to z scores using the standard deviations from equation (7.35), as shown in table 7.4.

It is worth noting here that interpretation of joins count results can be a little confusing, since not all the results will be consistent with the type of autocorrelation. In this example, the number of WW joins is about what would be expected (a little low, but not far from expectations). Nevertheless, the unexpectedly high number of BB joins, and unexpectedly low number of BW joins are both indicative of positive autocorrelation so we conclude that the map is positively autocorrelated.

LESSON 8: SPATIAL AUTOCORRELATION

Commentary - Chapter 7, Section 7.6, "Other Measures of Spatial Autocorrelation"

Problems with joins counting are evident. In particular, it does not work for numeric data. Other measures have been developed for numerical data, and, in practice, these are much more widely used.

While the equations for both Moran's I (pages 197-201) and Geary's c (page 201) look intimidating, they make a great deal of sense. Both consist of

• a measure of similarity,
• a mechanism that includes only those map units that are near to one another in the calculation, and
• a weighting factor that scales the resulting calculation so that it is in a standard numerical range.

In the case of Moran's I, the similarity measure is the standard method uses in correlation statistics, namely the product of the differences in each value from the mean. This produces a positive result when both the value and neighboring values are higher or lower than the mean and a negative result when the value and neighboring values are on opposite sides of the mean (one higher, the other lower).

For Geary's c the similarity measure is the squared difference in the two values.

In each case, the difference measure is summed over all neighboring pairs of map units (this is where the w_ij values from a weights matrix come in) and then adjusted so that the resulting index value is in a standard numerical range.

Using other Weight Matrices, pages 201-3

The inclusion of spatial interaction weights between pairs of map units in the formulas for calculating I and c means that it is possible to experiment with a wide variety of autocorrelation measures by tailoring the particular choice of interaction weights appropriately.

You will be able to explore these possibilities in this week's project using the GeoDa software.

LESSON 8: SPATIAL AUTOCORRELATION

Commentary - Chapter 7, Section 7.7, "Local Indicators of Spatial Association"

The final topic in measuring spatial autocorrelation is LISA or Local Indicators of Spatial Association.

All the previously discussed measures of spatial autocorrelation share the common weakness that they do not identify specific locations on a map where the measured autocorrelation is most pronounced. That is, they are global measures, which tell us that the map data are autocorrelated but not where to find the data that contribute most to that conclusion. Equally, global measures do not allow us to identify map regions where the pattern runs counter to the overall autocorrelation trend.

LISA statistics address these failings and exemplify a trend in spatial analysis in favor of approaches that emphasize local effects over global ones. (See the papers by Unwin 1996 and Fotheringham 1997 cited in the text for more details on this trend.)

The LISA approach simply involves recording the contributions from individual map units to the overall summary measure whether it is Moran's I or Geary's c.

Significance tests on LISA statistics are hard to calculate and generally depend on Monte Carlo simulation, as was previously discussed in the context of point pattern analysis (see Lesson 4). The idea is that a computer can randomly rearrange the map unit values many times, measuring the LISA statistic for each map unit each time, and then determine if actual observed LISA values are unusual with respect to this simulated distribution of values.

LESSON 8: SPATIAL AUTOCORRELATION

Final Activities for Lesson 8

Now that you've completed the readings and the self-test quiz for this lesson, it is time to apply what you've learned!

The following links will open in a new browser window.

1. Complete Project 8. This week's project explores ethnic residential segregation in Auckland, New Zealand using spatial autocorellation measures provided by the GeoDa tool. (The materials for Project 8 can be found under the Lessons tab, in the Lesson 8 folder.) Email your completed writeup to me.
2. Continue the Quarter-long Project by posting evidence of your progress this week. See the Week 8 directions for details.

PROJECT 8: SPATIAL AUTOCORRELATION ANALYSIS USING GEODA

Overview

Background

This week's project uses not a GIS program, but a package for exploratory spatial data analysis, called GeoDa. GeoDa is a good example of current research software, which implements many methods that have been in the academic research literature for several years, but which have yet to make it into standard desktop GIS tools. Among the methods it offers are simple measures of spatial autocorrelation.

You will use GeoDa to examine the spatial distribution of different ethnic groups in Auckland, New Zealand (where I live).

Until the last 20 years or so, Auckland was a relatively 'sleepy' industrial port. It has been New Zealand's largest city for about a century, but its dominance of the national economy has become even more marked in recent years. This is partly attributable to increasing numbers of immigrants to New Zealand, almost all of whom have settled in the Auckland region. Today, Auckland accounts for about one third of the total population of the country (about 1.35 million people depending on where you think the city stops), and for a much larger fraction of the more recent migrant groups. Auckland is the largest Pacific Islander city in the world, and also home to large populations of M
ori (the pre-European indigenous people), and Asian peoples, alongside the majority European-descended (or, in M
ori, 'Pakeha') 'white' population.

Such rapid change is exciting (it has certainly improved the food in Auckland!), but can also lead to strains and tensions between and within communities. We can't possibly explore all that is going on in a short project like this, but hopefully you will get some flavor of the city from this exercise.

The basic analytical approach adopted in this project is very similar to that presented by Andrea Frank in an article:

'Using measures of spatial autocorrelation to describe socio-economic and racial residential patterns in US urban areas' pages 147-62 in Socio-Economic Applications of Geographic Information Science edited by David Kidner, Gary Higgs and Sean White (Taylor and Francis, London), 2002.

This week's project is deliberately more like a short exercise than some of the earlier projects. This is for two reasons. First, you should be spending an increasing amount of time on your quarter-long project. Second, we will cover some ideas in this project not covered in class, and also introduce a new tool. If you want to explore these ideas and the GeoDa tool further then I hope that this exercise will give you an idea where to start!

Project Resources

The zip file you need for Project 8, project8materials.zip, is available here for download. (That file is 3.4 Mb and will take approximately 8 minutes to download over a 56 Kbps modem.) If you have any difficulty downloading this file, please contact me.

The contents of this archive are as follows:

• ak_CAU01_ethnic shapefiles showing the greater Auckland region delineated by the New Zealand 2001 Census Area Units (CAUs).  CAUs are roughly equivalent to tracts in the US census, with a few thousand people in each CAU.  There are 355 of these in the greater Auckland region. The data table for this shapefile contains counts and percentages of the population in each of five groups (European, M
  ori, Pacific Islander, Asian, and 'Other').
• akCity_CAU01_ethnic shapefiles showing the 101 CAUs of the central Auckland 'City' region. This area contains the CBD and many of the more upscale neighborhoods of the city. The ethnicity count and percentage data are repeated in these files.
• akCity_MB01_ethnic shapefiles showing 2001 Census 'Mesh Blocks' for the City area. Mesh Blocks (MBs) are the smallest areal unit used in the New Zealand census with no more than a few hundred people in each. There are almost 3000 MBs in the City area alone.
• ak_DEM_100 raster digital elevation model files that will give you some idea of the topography of the city although this is for interest only and has no effect on the details of the project.
• nz_coastline shapefiles are also for interest only and will give you some context for Auckland's location relative to the country as a whole (it's 'near the top'!).
• Three GAL files showing contiguity for the census shapefiles. These are used by GeoDa to perform autocorrelation analysis and will be explained in more detail in the project instructions.

You will also need a copy of the GeoDa software in order to run the required analysis for this project. GeoDa is available for download from the Spatial Analysis Laboratory (SAL) at the University  of Illinois at Urbana-Champaign here: https://www.geoda.uiuc.edu/downloadin.php. If you have trouble with that link, try this one: https://netfiles.uiuc.edu/koschins/shared/GeoDa.exe or this one https://www.geoda.uiuc.edu/downloads/geoda_downloads#new. Instructions for installing GeoDa are also available from the SAL website. Version 0.9.5-i of GeoDa was current at the time of writing and was used to prepare these project instructions, so where possible, this is the version you should use.

Summary of Project 8 Deliverables

For Project 8, the items you are required to have in your write-up are:

•  For a single variable on a single map, describe the results of a global Moran's spatial autocorrelation analysis. Include a choropleth map and Moran's scatter plot along with commentary and your interpretation of the results. In particular, identify map areas that contribute strongly to the global outcome.
• For a single variable on a single map (but a different variable and a different map from the last one), describe results of a univariate LISA analysis. Include the Cluster map and Moran's scatter plot in your write-up along with commentary and your interpretation of the results.

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Project 8 thread on the Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the In Touch tab, above, and then scrolling down to the Discussion Forums section.)

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 8: SPATIAL AUTOCORRELATION ANALYSIS USING GEODA

GeoDa Basics

Once installed, you run GeoDa by clicking an icon or double-clicking a shortcut in the usual way. If the GeoDa installer did not make an entry in the Start Menu, you can create a shortcut by navigating to c:\Program Files\GeoDa\geoda095i.exe then right-clicking and selecting Create Shortcut.

When GeoDa starts up, open a shapefile from the File - Open Project menu selection and navigate to the shapefile you want to look at. The Key Variable setting in the GeoDa Project Setting dialog (below) is not important and can be left as the default selection.

The GeoDa Project Setting dialog.

Making maps in GeoDa is simple: select the type of map you want from the Map menu. With the datasets you are working with in this project, only the first four options, Quantile, Percentile, Box Map and St Dev. make sense. Each of these makes a choropleth with the class intervals based on a different statistical view of the data (recall the project in Lesson Two).

In the current version of GeoDa (Version 0.9.5-i), I have been unable to get the Cartogram to work with the Census Area Unit shapefiles used in this project. I believe that this is a problem with the shapefiles, and not with GeoDa. Specifically, when ArcGIS is used to aggregate polygon shapefiles from smaller units (here, I made the CAUs from the mesh block data) it often shifts polygon boundaries sufficiently that they no longer touch one another. The cartogram tool relies on polygons touching one another for its simplified picture of the map. If you are interested in making a cartogram the akCity_MB01_ethnic shapefile works, or try the sample data sets supplied with GeoDa.

The main focus of GeoDa is exploratory spatial data analysis (ESDA). To get a flavor of this, try making a histogram or scatterplot using the named options in the Explore menu. Once you have a histogram or scatterplot in one window, you can select data points in the statistical display, and see those selections highlighted in the map views.  In general, any selection in any window in GeoDa will be highlighted in all map views. This is called linked-brushing and is a key feature of exploratory data analysis.

Linked brushing can help you to see patterns in spatial data more readily, particularly spatial autocorrelation effects. When data is positively spatially autocorrelated moving the 'brush' in an area in a statistical display (say a scatterplot) will typically show you sets of locations in the map views that are also close together. Moving the brush around can help you to spot cases that do not follow the trend.

For a moving brush, make a selection in any view while holding down the <CTRL> key. Once you have made the selection, you can let go of the <CTRL> key and then move the selection area around by dragging with the mouse. To stop the moving selection, click again, anywhere in the current view.

Of course, as you are well aware, seeing a pattern is not the same as it really being there. In the case of autocorrelation, that is the role of the measures we have covered in this lesson's reading, and in particular, Moran's I, which we will look at more closely in the remainder of this project.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 8: SPATIAL AUTOCORRELATION ANALYSIS USING GEODA

Global Autocorrelation

While GeoDa is like a GIS, you will soon find its cartographic capabilities somewhat limited. Where it really comes into its own is in the integration of spatial analysis methods with mapping tools.

Contiguity matrices

To determine the spatial autocorrelation of a variable globally across a map using Moran's I, you access the Spatial - Univariate Moran menu. However, before doing this, you need a representation of the contiguity structure of the map, that is, which map units are neighbors to each other. This provides the w_ij values for the Moran's I calculation to determine which pairs of attribute values should be included in the correlation calculation.

GeoDa provides tools for creating contiguity matrices under the Tools - Weights > Create menu option. Selecting this option opens the CREATING WEIGHTS dialog:

The GeoDa CREATING WEIGHTS dialog box

The various options available here are explained in the GeoDa documentation. For the purposes of this project I have already created simple contiguity matrix files called ak_CAU01.gal, akCity_CAU01.gal and akCity_MB01.gal. It is instructive to examine (but don't edit!) these files in a text editor. For example, if you open akCity_CAU, the first few lines look like this:

101
1 6
3 5 21 23 25 28
2 4
3 4 21 34
3 5
1 2 4 5 21
4 5
2 3 5 6 34
5 7
1 3 4 6 25 28 29

The first line here shows how many areal units there are in the associated shapefile, in this case the 101 CAUs in Auckland City. Each pair of lines after that has the following format.

• First is an ID number for an areal unit followed by the number of neighbors it has. In this case, the CAU with ID number (in fact, just a sequence number) 1, has 6 neighbors.
• In the next line the sequence numbers of these are identified as 3, 5, 21, 23, 25 and 28.

A more complete explanation of alternative formats for GAL and GWT formats (the latter allows weighted contiguities based on inverse distance and so on) is provided in the GeoDa documentation.

The real reason I have provided pre-calculated GAL files is that the previously mentioned problem with the CAU shapefiles (see the previous page) prevents GeoDa from successfully calculating them itself. I was able to get around the problem using the R statistical software with the spdep, shapefile and maptools packages. If you ever face a similar problem you may also find this helpful. spdep provides a method for calculating GAL files that includes a tolerance, so that areal units within a specified 'snap' distance of one another are considered neighbors.

Calculating Global Moran's I and the Moran Scatterplot

This is easy. Select the Space - Univariate Moran menu option and specify the variable to use, and the contiguity matrix to use. GeoDa will think for a while, and then present you with a display that shows the calculated value of Moran's I and a scatterplot.

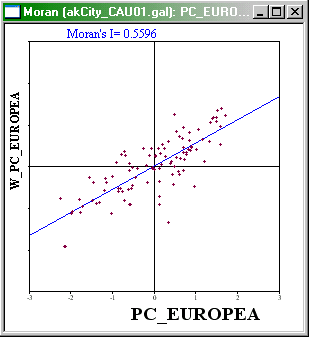
Moran Scatterplot showing relationship between a variable and the average value of its neighbors for the same variable.

The Moran Scatterplot is an illustration of the relationship between the values of the chosen attribute at each location and the average value of the same attribute at neighboring locations. In the case shown, large Percentages of Europeans (points on the right hand side of the plot) tend to be associated with high local average values of Percentage of Europeans (points toward the top of the plot).

It is instructive to consider each quadrant of the plot. In the upper-right quadrant are cases where both the value and local average value of the attribute are higher than the overall average value. Similarly in the lower-left quadrant are cases where both the value and local average value of the attribute are lower than the overall average value. These cases confirm positive autocorrelation. Cases in the other two quadrants indicate negative autocorrelation. depending on which groups are dominant, there will be an overall tendency towards positive or negative (or perhaps no) autocorrelation.

Using linked brushing, you should be able to identify which areas of the map are most responsible for high or low observed autocorrelation, and which, if any, locations run counter to the overall pattern.

For a single variable on a single map, describe the results of a global Moran's spatial autocorrelation analysis in your write-up. Include a choropleth map and Moran's scatter plot in your write-up along with commentary and your interpretation of the results. In particular, identify map areas that contribute strongly to the global outcome.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 8: SPATIAL AUTOCORRELATION ANALYSIS USING GEODA

Local Indicators of Spatial Association

We saw in the context of point pattern analysis that deriving a global, whole-map measure is often not the thing of most interest to analysts. Rather, it may be more important to know which local features in the data are contributing most strongly to the overall pattern. In the context of point pattern analysis, this is a relatively simple notion: if the pattern is clustered, then finding the clusters is the key. If the data is evenly-spaced, then by definition, this is a global feature.

In the context of spatial autocorrelation, the localized phenomena of interest are those areas on the map that contribute particularly strongly to the overall trend (which is usually positive autocorrelation). Methods that enable an analyst to identify localized map regions where data values are strongly positively or negatively associated with one another are collectively known as Local Indicators of Spatial Association (or LISA).

Again, GeoDa has a built in capability to calculate LISA statistics, and provide useful interactive displays of the results.

How LISA works

The menu option in GeoDa is Space - Univariate LISA . The easiest way to learn how LISA works is to run it:

1. Select the Space - Univariate LISA menu option. In the dialog boxes that appear, specify the variable to use, and the spatial weights file (i.e., the GAL file).
2. Request the Moran Scatterplot, the Significance Map, and the Cluster Map.
3. GeoDa will think for a moment and then produce three new displays. You can sort them out by selecting the Window - Tile Horizontal menu option. You should end up with something like this:

The GeoDa window after running LISA. Note that the map view here (bottom right) was present before LISA was run.

The meaning of each of these displays is considered in the next sections.

Moran's Scatterplot

This display is exactly the same one as produced previously using simple Moran's I. By linking and brushing between this and other displays you may be able to develop an understanding of what they are showing you.

LISA Cluster Map

The LISA cluster map looks like this:

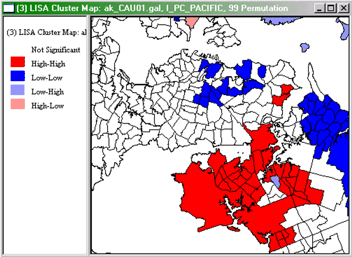
GeoDa LISA Cluster map for Percent Pacific Islanders in Auckland Region CAUs, 2001.

Interpretation of this map is straightforward. Red highlighted regions have high values of the variable and have neighbors with high values also (high-high). As indicated in the legend, blue area are low-low in the same scheme, while pale blue regions are low-high and pink areas are high-low. The strongly colored regions are therefore those that contribute significantly to a positive global spatial autocorrelation outcome, while paler colors contribute significantly to a negative autocorrelation outcome.

By right-clicking in this view, you can affect which cases are displayed, opting to see only those that are most significant. The relevant menu option is the Significance Filter. The meaning of this will become clearer when we consider the LISA Significance Map.

LISA Significance Map

The LISA Significance Map is shown below:

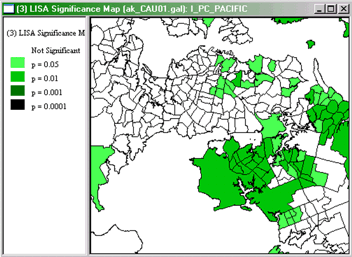
GeoDa LISA Significance Map for Percent Pacific Islanders in Auckland Region CAUs, 2001.

This display shows the statistical significance level at which each region can be regarded as making a meaningful contribution to the global autocorrelation outcome.

This is determined using a rather complex Monte Carlo randomization procedure (recall Monte Carlo methods from Lesson 4, where they were discussed in relation to GAM):

• The LISA value for each location is determined from its individual contribution to the global Moran's I calculation, as discussed on pages 203-5 of the course text.
• Whether or not this value is statistically significant is assessed by comparing the actual value to the value calculated for the same location by randomly reassigning the data among all the areal units and recalculating the values each time.
• Actual LISA values are ranked relative to the set of values produced by this randomization process.
• If an actual LISA score is among the top 0.1% (or 1% or 5%) of scores associated with that location under randomization, then it is judged statistically significant at the 0.001 (or 0.01 or 0.05) level. Note that a statistically significant result may be either very high or very low.

The combination of the Cluster Map and the Significance Map allows you to see which locations are contributing most strongly to the global outcome and in which direction.

By adjusting the Significance Filter in the Cluster Map you can see only those areas of highest significance. By selecting the Randomization right-click menu option and choosing a larger number of permutations (the default is 99), you can test just how strongly significant are the high-high and low-low outcomes seen in the Cluster Map.

I know that this is all rather complicated. Feel free to post questions to this week's Discussion Forums if you are not following things. Your colleagues may have a better idea of what is going on than you do! Failing that, as usual, I will respond to messages posted to the boards to help clear up any confusions.

For a single variable on a single map (but a different variable and a different map from the last one), describe the results of a univariate LISA analysis. Include the Cluster map and Moran's scatter plot in your write-up along with commentary and your interpretation of the results.

Ready to continue? Click on the "Next" link, above, to continue with this project.

PROJECT 8: SPATIAL AUTOCORRELATION ANALYSIS USING GEODA

Checklist of Project 8 Deliverables

Here is a summary of the deliverables for Project 8, to be posted as a PDF (preferably) or MS Word document. Once posted, please provide a link to the document in the discussion forum "Posted project links" thread for this week. Note that if you don't have access to any webspace for posting, that you can simply attach the document to your post to the discussion forum. Make sure you have completed each item!

1.  For a single variable on a single map, insert into your write-up results of a global Moran's spatial autocorrelation analysis. Include a choropleth map and Moran's scatter plot in your write-up along with commentary and your interpretation of the results. In particular, identify map areas that contribute strongly to the global outcome.
2. For a single variable on a single map (but a different variable and a different map from the last one), insert into your write-up results of a univariate LISA analysis. Include the Cluster map and Moran's scatter plot in your write-up along with commentary and your interpretation of the results.

That's it for Project 8!

End of Project 8 - Remember, if you have any questions, post them to the appropriate Discussion Forum.

QUARTER-LONG PROJECT

Week 8: Posting Evidence of Your Progress (Part 2)

No, really... don't leave it until the last minute! To show me that you are continuing to make progress on your quarter-long project, I want you to post another piece of evidence to your web site. Again, timely submission of such evidence is worth 1 of the 30 total points available for the quarter-long project.

There is no specific output required as this will vary from project to project. The aim of this week activity is that you continue to feel some pressure to work on the project and not leave it all until the last minute.

Post something that is evidence of your progress (a screenshot is probably easiest) to your web site, as part of the "Quarter-long Project" section of your site. Use the course email system to notify the instructor that you have done this including a URL.

Questions?

If you have any questions now or at any point during this project, please feel free to post them to the Quarter-long Project Discussion Forum. (That Discussion Forum can be accessed at any time by clicking on the In Touch tab, above, and then scrolling down to the Discussion Forums section.)

That's it for the quarter-long project this week!